Happy Tau Day, the most exciting math holiday you’ve yet to discover! Today, June 28th is 6/28, which contains in order the first three digits of tau (τ), the rival of math’s most popular irrational number, pi (π).
In 2001, Bob Palais wrote an article for The Mathematical Investigator called ,“π is wrong!” In it, he insists that the choice of using π in our mathematical formulas for hundreds of years is no good. He argues that the use of τ would simplify many formulas and its derivation is much more intuitive. (Notice that the symbol resembles that for pi, but with one "leg" instead of two.)
The significance of our beloved irrational number π is that it is equal to the ratio of the circumference of any circle to its diameter--in notation, π = C/d. However, the most defining characteristic of a circle is not its diameter but its radius. A circle is defined as the collection of points on a plane that are exactly the same distance, its radius, from a point, its center. Palais argues that intuition should direct us to the use of a more elegant Circle Constant, tau, where τ is the ratio of the circumference of a circle to its radius--in notation, τ = C/r.
Self-described “notorious mathematical propagandist” Michael Hartl takes the argument even further in his now-famous “The Tau Manifesto,” which he published on Tau Day of 2010, exactly one year ago. He demonstrates with many adapted formulas that the factor of 2 is unnecessary if we incorporate it into the ratio itself. For instance, the periods of basic trigonometric functions f(x) = sin(x), and f(x) = cos(x), are in both cases 2π. Why not change them to tau instead? Palais and Hartl each list numerous other examples from calculus and physics, in which the factor of 2 is rendered obsolete by replacing 2π with τ.
The really intuitive part is revealed if you think of angle measure. How things are done now with π, a half turn of the circle is π radians, and a full turn is 2π radians. Should we adopt τ instead, τ radians would be a full turn, τ/2 radians a half turn, τ/4 radians a quarter turn, and so on.
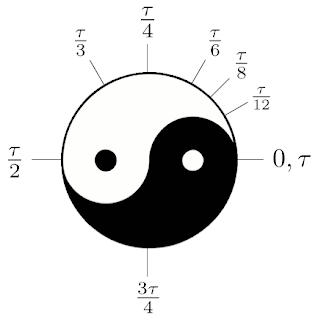
There are, of course, instances where π appears un-doubled. For instance, the formula for area of a circle: A = πr2. Hartl shows, in a mathematically sophisticated way, that the replacement of π by τ even in this instance is the more sound choice, since it is analogous to similar formulas in physics.
An article in today’s BBC News paints the issue as a violent conflict, with pi detractors up in arms over a lifetime of educational betrayal, which seems to this mathematician something of a manufactured controversy. (I can imagine you'd be upset if you are the sort of mathematician that has memorized pi to the nth digit. If you are one of these folks, here's the start for your new parlor trick: reciting tau, 6.283185307...) 
Is it worthwhile to switch to tau use, an
2 Comments on Is Tau Better Than Pi? Irrational Arguments, last added: 6/29/2011
Display Comments
Add a Comment
I love this story because I think it eloquently demonstrates the following dispositi
Teachers should expect to be questioned about this: “Why not clockwise?” The stock answer is, “That’s the rule.” Take the time to delve a little deeper. This response may sound to a young person like, “because I say so.” Dissatisfaction with explanations and confusion about them go hand in hand. A solid understanding of how to label the quadrants should enable your students to discuss graphing more efficiently. Graphing on the coordinate plane is a skill that will be immensely valuable throughout high school math and well into college courses, including and beyond multi-variable calculus and electro physics. The purpose of this convention and most conventions in general, is to avoid ambiguity. (And ambiguity can lead to chaos! Imagine if we didn’t have the convention of driving on only one side of the road.) 
Physicists in particular use the 
Great post. I almost forgot about tau since 6/28 is a special day for me. I guess the debate will go on, but probably not much change.
You have explained this so well! I would like to try replacing pi with tau when I cover circles with my students. It will be a great opportunity for them to take a position and argue it one way or the other.