Viewing: Blog Posts Tagged with: puzzle, Most Recent at Top [Help]
Results 1 - 25 of 47
Blog: wonkyworks (Login to Add to MyJacketFlap)
JacketFlap tags: abc, alphabet, free children's kindle picture book, free ebook for kids, kindle silly monsters rhyming ABC alphabet picture book, puzzle, Add a tag
Blog: wonkyworks (Login to Add to MyJacketFlap)
JacketFlap tags: monsters, puzzle, children's kindle picture book silly monster abc, odd one out, puzzle monsters, Add a tag
Blog: wonkyworks (Login to Add to MyJacketFlap)
JacketFlap tags: crumhorn, illustration, puzzle, Add a tag
Blog: Sparky Firepants Art Blog (Login to Add to MyJacketFlap)
JacketFlap tags: puzzle, tofu, coloring, maze, How, sauna, adult coloring, Add a tag
In my quest to fill the world with the happiest, weirdest art in the world, I have dreamed up yet another vehicle for the task: A coloring and activity book!
While it’s in the works, I couldn’t resist sharing some of the pages with you. Here’s one that will both scratch your coloring itch and stave off Alzheimer’s. It’s printable on regular letter-sized paper (select Fit to Page for best results). Enjoy!
Blog: Whateverings (Login to Add to MyJacketFlap)
JacketFlap tags: paulajbecker, letter P, party, kids, General Illustration, Samples, puzzle, paula becker, park, Focus on the Family, Cartoons & Comics, Clubhouse Jr. magazine, Add a tag
New back-page puzzle for Clubhouse Jr….
Blog: Whateverings (Login to Add to MyJacketFlap)
JacketFlap tags: Cartoons & Comics, dog walking, paulajbecker, pirate boy, kids, cartoon, General Illustration, children's illustration, Samples, puzzle, paula becker, carrot, horse, Add a tag
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: Books, Philosophy, puzzle, paradox, Paradoxical, *Featured, yablo paradox, Arts & Humanities, Roy T. Cook, philosophy puzzle, Roy Cook, Add a tag
The collection of infinite Yabloesque sequences that contain both infinitely many Y-all sentence and infinitely many Y-exists sentences, however, is a much larger collection. It is what is called continuum-sized, and a collection of this size is not only infinite, but strictly larger than any countably infinite collection. Thus, although the simplest cases of Yabloesque sequence – the Yablo Paradox itself and its Dual – are paradoxical, the vast majority of mixed Yabloesque sequences are not!
The post Mixed Yablo Paradoxes appeared first on OUPblog.
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: Philosophy, pattern, puzzle, logic, paradox, Editor's Picks, *Featured, yablo paradox, Arts & Humanities, Roy T. Cook, generalization, maths puzzle, Paradox of generalizations, philosophy puzzle, Roy Cook, Books, Add a tag
A generalization is a claim of the form: (1) All A’s are B’s. A generalization about generalizations is thus a claim of the form: (2) All generalizations are B. Some generalizations about generalizations are true. For example: (3) All generalizations are generalizations. And some generalizations about generalizations are false. For example: (4) All generalizations are false. In order to see that (4) is false, we could just note that (3) is a counterexample to (4).
The post The paradox of generalizations about generalizations appeared first on OUPblog.
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: Perfection, forgery, paradox, yablo paradox, Roy T. Cook, *Featured, Arts & Humanities, Books, Philosophy, money, truth, puzzle, Add a tag
Imagine that Banksy, (or J.S.G. Boggs, or some other artist whose name starts with “B”, and who is known for making fake money) creates a perfectly accurate counterfeit dollar bill – that is, he creates a piece of paper that is indistinguishable from actual dollar bills visually, chemically, and in every other relevant physical way. Imagine, further, that our artist looks at his creation and realizes that he has succeeded in creating a perfect forgery. There doesn’t seem to be anything mysterious about such a scenario at first glance – creating a perfect forgery, and knowing one has done so, although extremely difficult (and legally controversial), seems perfectly possible. But is it?
In order for an object to be a perfect forgery, it seems like two criteria must be met. First of all, the object must be a forgery – that is, the object cannot be a genuine instance of the category in question. In this case, our object, which we shall call X, must not be an actual dollar bill:
1.) X is not a dollar bill.
Second, the object must be perfect (as a forgery) – that is, it can’t be distinguished from actual instances of the category in question. We can express this thought as follows:
2.) We cannot know that X is not a dollar bill.
Now, there is nothing that prevents both (1) and (2) from being simultaneously true of some object X (say, our imagined fake dollar bill). But there is an obstacle that seemingly prevents us from knowing that both (1) and (2) are true – that is, from knowing that X is a perfect forgery.
Imagine that we know that (1) is true, and in addition we know that (2) is true. In other words, the following claims hold:
3.) We know that X is not a dollar bill.
4.) We know that we cannot know that X is not a dollar bill.
Knowledge is factive – in other words, if we know a claim is true, then that claim must, in fact, be true. Applying this to the case at hand, this means that claim (4) entails claim (2). But claim (2) and claim (3) are incompatible with each other: (2) says we cannot know that X isn’t a dollar, while (3) says we know it isn’t. Thus, (3) and (4) can’t both be true, since if they were, then a contradiction would also be true (and contradictions can’t be true).

Thus, we have proven that, although perfect forgeries might well be possible, we can never know, of a particular object, that it is a perfect forgery. But an important question remains: If this is right, then what, exactly, is going on in the story with which we began? How is it that our imagined artist doesn’t know that he has created a perfect forgery?
In order to answer this question, it will help to flesh out the story a bit more. So, once again imagine that our artist creates the piece of paper that is visually, chemically, and in every other physical way indistinguishable from a real dollar bill. Call this Stage 1. Now, after admiring his work for a while, imagine that the artist then pulls eight genuine, mint-condition dollar bills out of his wallet, throws them on the table, and then places the forgery he created into the pile, shuffling and mixing until he can no longer identify which of the pieces of paper is the one he created, and which are the ones created by the Mint. Let’s call this Stage 2. How do Stage 1 and Stage 2 differ?
At Stage 1 we do not, strictly speaking, have a case of a perfect forgery. Although the piece of paper the artist created is physically indistinguishable from a dollar bill, the artist can nevertheless know it is not a dollar bill because he knows that he created this particular object. In other words, at Stage 1 he can tell that the forgery is a forgery because he knows the history, and in particular the origin, of the object in question.
Stage 2 is different, however. Now the fake is a perfect forgery, since it still isn’t a dollar, but we can’t know that it isn’t a dollar, since we can no longer distinguish it from the genuine dollars in the pile. So in some sense we know that the fake dollar in the pile is a perfect forgery. But we can’t point to any particular piece of paper and know that it, rather than one of the other eight pieces of paper, is the perfect forgery. In other words, in Stage 2 the following is true:
- We know there is an object in the pile that is a perfect forgery.
But the following, initially similar looking claim, is false:
- There is an object in the pile that we know is a perfect forgery.
We can sum all this up as follows: We can know that perfect forgeries exist – that is, we can know claims of the form “One of those is a perfect forgery”. But we can’t know, of a particular object, that it is a perfect forgery – that is, we can never know claims of the form “That is a perfect forgery”. And it is this latter sort of claim – that we know, of a particular object, that it is a perfect forgery – that leads to the contradiction.
The post The impossibility of perfect forgeries? appeared first on OUPblog.
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: mathematical truth, mind puzzle, why study paradoxes, Philosophy, Lies, trust, truth, puzzle, justice, guilt, paradox, maths, blame, Accusation, paradoxes, yablo paradox, Roy T. Cook, Books, Mathematics, Editor's Picks, *Featured, Arts & Humanities, Add a tag
One of the central tasks when reading a mystery novel (or sitting on a jury) is figuring out which of the characters are trustworthy. Someone guilty will of course say they aren’t guilty, just like the innocent – the real question in these situations is whether we believe them.
The guilty party – let’s call her Annette – can try to convince us of her trustworthiness by only saying things that are true, insofar as such truthfulness doesn’t incriminate her (the old adage of making one’s lies as close to the truth as possible applies here). But this is not the only strategy available. In addition, Annette can attempt to deflect suspicion away from herself by questioning the trustworthiness of others – in short, she can say something like:
“I’m not a liar, Betty is!”
However, accusations of untrustworthiness of this sort are peculiar. The point of Annette’s pronouncement is to affirm her innocence, but such protestations rarely increase our overall level of trust. Either we don’t believe Annette, in which case our trust in Annette is likely to drop (without affecting how much we trust Betty), or we do believe Annette, in which case our trust in Betty is likely to decrease (without necessarily increasing our overall trust in Annette).
Thus, accusations of untrustworthiness tend to decrease the overall level of trust we place in those involved. But is this reflective of an actual increase in the number of lies told? In other words, does the logic of such accusations makes it the case that, the higher the number of accusations, the higher the number of characters that must be lying?
Consider a group of people G, and imagine that, simultaneously, each person in the group accuses one, some, or all of the other people in the group of lying right at this minute. For example, if our group consists of three people:
G = {Annette, Betty, Charlotte}
then Betty can make one of three distinct accusations:

“Annette is lying.”
“Charlotte is lying.”
“Both Annette and Charlotte are lying.”
Likewise, Annette and Charlotte each have three choices regarding their accusations. We can then ask which members of the group could be, or which must be, telling the truth, and which could be, or which must be, lying by examining the logical relations between the accusations made by each member of the group. For example, if Annette accuses both Betty and Charlotte of lying, then either (i) Annette is telling the truth, in which case both Betty and Charlotte’s accusations must be false, or (ii) Annette is lying, in which case either Betty is telling the truth or Charlotte is telling the truth (or both).
This set-up allows for cases that are paradoxical. If:
Annette says “Betty is lying.”
Betty says “Charlotte is lying.”
Charlotte says “Annette is lying.”
then there is no coherent way to assign the labels “liar” and “truth-teller” to the three in such a way as to make sense. Since we are here interested in investigating results regarding how many lies are told (rather than scenarios in which the notion of lying versus telling the truth breaks down), we shall restrict our attention to those groups, and their accusations, that are not paradoxical.
The following are two simple results that constraint the number of liars, and the number of truth-tellers, in any such group (I’ll provide proofs of these results in the comments after a few days).
“Accusations of untrustworthiness tend to decrease the overall level of trust we place in those involved”
Result 1: If, for some number m, each person in the group accuses at least m other people in the group of lying (and there is no paradox) then there are at least m liars in the group.
Result 2: If, for any two people in the group p1 and p2, either p1 accuses p2 of lying, or p2 accuses p1 of lying (and there is no paradox), then exactly one person in the group is telling the truth, and everyone else is lying.
These results support an affirmative answer to our question: Given a group of people, the more accusations of untrustworthiness (i.e., of lying) are made, the higher the minimum number of people in the group that must be lying. If there are enough accusations to guarantee that each person accuses at least n people, then there are at least n liars, and if there are enough to guarantee that there is an accusation between each pair of people, then all but one person is lying. (Exercise for the reader: show that there is no situation of this sort where everyone is lying).
Of course, the set-up just examined is extremely simple, and rather artificial. Conversations (or mystery novels, or court cases, etc.) in real life develop over time, involve all sorts of claims other than accusations, and can involve accusations of many different forms not included above, including:
“Everything Annette says is a lie!”
“Betty said something false yesterday!”
“What Charlotte is about to say is a lie!”
Nevertheless, with a bit more work (which I won’t do here) we can show that, the more accusations of untrustworthiness are made in a particular situation, the more of the claims made in that situation must be lies (of course, the details will depend both on the number of accusations and the kind of accusations). Thus, it’s as the title says: accusation breeds guilt!
Note: The inspiration for this blog post, as well as the phrase “Accusation breeds guilt” comes from a brief discussion of this phenomenon – in particular, of ‘Result 2′ above – in ‘Propositional Discourse Logic’, by S. Dyrkolbotn & M. Walicki, Synthese 191: 863 – 899.
The post Accusation breeds guilt appeared first on OUPblog.
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: Books, Philosophy, puzzle, Quaker Oats, paradox, Editor's Picks, *Featured, yablo paradox, Arts & Humanities, Impossible Painting, Liar paradox, Roy T. Cook, Russell paradox, Add a tag
Supposedly, early 20th century packaging for Quaker Oats depicted the eponymous Quaker holding a package of the oats, where the art on this package depicted the Quaker holding a package of the oats, which itself depicted the Quaker holding a package of the oats, ad infinitum. I have not been able to locate an photograph of the packaging, but more than one philosopher and mathematician has attributed an early interest in the nature of the infinite to childhood contemplation of this image. Here, however, I want to examine a different phenomenon: whether artwork that depicts itself in this way can lead to paradoxes.
Let’s begin with two well-known puzzles. The older of the two– the Liar paradox – was known to ancient Greek philosophers, and challenges the following platitudes about truth:
(T1) A sentence is true if and only if what it says is the case.
(T2) Every sentence is exactly one of true and false.
Consider the Liar sentence:
This sentence is false.
Is the Liar sentence true or false? If it is true, then what it says must be the case. It says it is false, so this means it is false. If it’s false, then, since it says it is false, what it says is indeed the case. But this would make it true. So the Liar sentence is true if and only if it is false, violating the platitudes.
The second puzzle is the Russell paradox, discovered by Bertrand Russell at the beginning of the 20th Century. This paradox involves collections, or sets, of objects, and two central theses:
(S1) Given any property P, there is a set of objects containing all and only the objects that have P.
(S2) Sets are themselves objects, and can be contained in sets.
Given (S2), we can divide objects into two types: Those that contain themselves (such as the set containing all sets whatsoever) and those that do not contain themselves (such as the set of all kittens). Thus, “is a set that does not contain itself” picks out a perfectly good property, and so by (S1) there should be a set – let’s call it R – containing exactly those things that have this property. So:
A set is a member of R if and only if it is not a member of itself.
Now, is R a member of itself? Either it is or it isn’t. If R is a member of itself then R isn’t a member of itself. And if R isn’t a member of itself then R is a member of itself. Either way, R both is and isn’t a member of itself. Again, a contradiction.

There is another puzzle that seems intimately connected to these two paradoxes, however, that has not (as far as I know) been noticed or studied – the paradox of the impossible painting. This paradox stems from two principles governing the notion of depiction (or representation) rather than truth or set-theoretic membership.
First, it seems, at least at first glance, that we can paint anything that we can describe – if I tell you to paint a forest with exactly 28 trees, then you can produce a painting fitting that description. Thus:
(D1) Given any description D, we can create a painting that depicts things exactly as described in D.
Second, there is nothing to prevent a painting from being depicted within another painting – for example, Velazquez’s Las Meninas depicts the painter working on another painting. Thus:
(D2) Paintings can be depicted in paintings.
If some paintings can depict other paintings, then it seems like we can divide paintings into two types: those that depict themselves (such as the artwork on old Quaker Oats packaging) and those that do not. Thus, “a scene depicting all and only the paintings that do not depict themselves” is a perfectly good description, and so by (D1) it should be possible to produce a painting – let’s call it I – that depicts things as described. So:
A painting is depicted in I if and only if it does not depict itself.
Should I depict itself ? In other words, if you are creating this painting, should you include a depiction of I itself within the scene? If you include I in the painting, then I is a painting that depicts itself, so it should not be depicted in I after all. But if you don’t include I in the painting, then I is a painting that does not depict itself, so it should have been included. Either way, you can’t create a painting that depicts things exactly as described.
The paradox of the impossible painting is distinct from both the Liar paradox and the Russell paradox, since it involves depiction rather than truth or set-membership. But it has features in common with each. Most obviously, circularity plays a central role in all three paradoxes: the Liar paradox involves sentences that says something about themselves, the Russell paradox involves sets that are members of themselves, and the paradox of the impossible painting involves paintings that depict themselves.
“Who knew oats could be so deep?”
Nevertheless, the paradox of the impossible painting has features not shared by the Liar paradox, and other features not shared by the Russell paradox. First, the Liar paradox involves a sentence that clearly exists (and is grammatical, etc.) that must be accounted for, while the Russell paradox can be seen in different terms, as a sort of proof that the Russell set R just doesn’t exist, and that we need to revise (S1) accordingly. The proper response regarding the paradox of the impossible painting is more like the latter – we are not tempted to think that the paradoxical painting does or could exist, but instead conclude that there is something wrong with (D1).
There is another sense, however, in which the paradox of the impossible painting is more like the Liar paradox than the Russell paradox. The Liar paradox arguably arises because of circularity of reference: the Liar sentence refers to, or ‘picks out’, itself. And the paradox of the impossible painting arises because of circularity of depiction – that is, paintings that depict, or ‘pick out’, themselves. Reference and depiction are different, but, insofar as they are both ways of ‘picking out’, while set-theoretic membership is not, suggests that, in this respect at least, the paradox of the impossible painting has more in common with the Liar paradox than with the Russell paradox.
Thus, the paradox of the impossible painting ‘lies between’, or is a sort of hybrid of, the Liar paradox and the Russell paradox, with some features in common with the former and others in common with the latter. As a result, studying this puzzle further seems likely to reward us with deeper insights into these two much older and more well-known conundra. Who knew oats could be so deep?
The post The impossible painting appeared first on OUPblog.
Blog: Topsy Turvy Land - Donna J. Shepherd (Login to Add to MyJacketFlap)
JacketFlap tags: Kevin Scott Collier, Donna Shepherd, Puzzle, Teacher, eBook, activity, donna j. shepherd, ouch sunburn, Skincare, Word Search, Sunburn, printable, NOOKbook, Add a tag
Click puzzle to enlarge and print. Find more information about the book HERE. Buy the NOOKbook: OUCH! Sunburn
Blog: Whateverings (Login to Add to MyJacketFlap)
JacketFlap tags: Links, kids, fun, cute, dog, comics, cartoons, dogs, cartoon, comic, General Illustration, children's illustration, Samples, leash, funny, puzzle, sweet, paula j. becker, paula becker, street, Cartoons & Comics, Add a tag
I’m working on and finishing up a few projects, and all have a dog or dogs. Also, in different styles. Below are clips from the final or working toward final illustrations.
Blog: Illustration for Kids Blog (Login to Add to MyJacketFlap)
JacketFlap tags: Illustration, kids, magazine, cartoon, children's illustration, puzzle, cleaning, paula j. becker, dinner, paula becker, raccoons, mother's day, Add a tag
Samples came the other day, of the fun Mother’s Day illustration I worked on for a back-page puzzle for Clubhouse Jr. magazine I had a lot of fun with this. I worked in a bit of a tighter style using a very thin line. I’m really pleased with how the final printed piece turned out. And the raccoons still make me smile! Below are some photos of the final art.
Blog: Illustration for Kids Blog (Login to Add to MyJacketFlap)
JacketFlap tags: airport, suitcases, people in line, Illustration, kids, comics, cartoon, children's illustration, baggage, puzzle, plane, paula j. becker, paula becker, Add a tag
I had some big illustration projects lately, and below is a little snip of one of the finished illustrations. Can you guess where the scene takes place? I think I made it too easy. : )
Blog: Whateverings (Login to Add to MyJacketFlap)
JacketFlap tags: children, Links, fun, art, drawing, pizza, hidden pictures, bunny, puzzle, Illustration For Kids, paula j. becker, paula becker, Highlights for Children, cafeteria, Cartoons & Comics, craft sale, Add a tag
Below are some glimpses of hidden picture illustrations either published or fresh off the drawing board. These are a challenge but really fun to do!
(c) Highlights For Children
Blog: Art & Drawings by Dain Fagerholm (Login to Add to MyJacketFlap)
JacketFlap tags: dain fagerholm, penrose, asylum maze game, puzzle, 3d, blue girl, app, kickstarter, ios, Add a tag
Pentode: a 3d maze game for iOS handhelds - main menu game demo ipad screen test 3/28/13 vine.co/v/bjdgdhuFIJU
— DAiN8) (@DainFagerholm) March 28, 2013
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: puzzles, puzzle, clues, Mathematics, sudoku, Jason Rosenhouse, *Featured, rosenhouse, Science & Medicine, Gary McGuire, Laura Taalman, Taking Sudoku Seriously, mcguire’s, creationists, Add a tag
By Jason Rosenhouse
Among mathematicians, it is always a happy moment when a long-standing problem is suddenly solved. The year 2012 started with such a moment, when an Irish mathematician named Gary McGuire announced a solution to the minimal-clue problem for Sudoku puzzles.
You have seen Sudoku puzzles, no doubt, since they are nowadays ubiquitous in newspapers and magazines. They look like this:
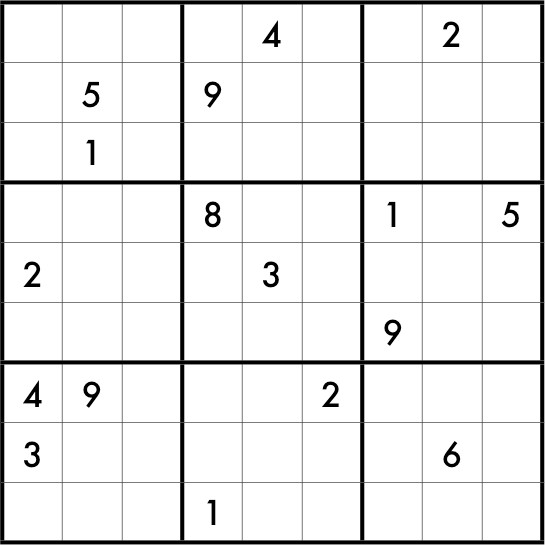
Your task is to fill in the vacant cells with the digits from 1-9 in such a way that each row, column and three by three block contains each digit exactly once. In a proper puzzle, the starting clues are such as to guarantee there is only one way of completing the square.
This particular puzzle has just seventeen starting clues. It had long been believed that seventeen was the minimum number for any proper puzzle. Mathematician Gordon Royle maintains an online database which currently contains close to fifty thousand puzzles with seventeen starting clues (in fact, the puzzle above is adapted from one of the puzzles in that list). However, despite extensive computer searching, no example of a puzzle with sixteen or fewer clues had ever been found.
The problem was that an exhaustive computer search seemed impossible. There were simply too many possibilities to consider. Even using the best modern hardware, and employing the most efficient search techniques known, hundreds of thousands of years would have been required.
Pure mathematics likewise provided little assistance. It is easy to see that seven clues must be insufficient. With seven starting clues there would be at least two digits that were not represented at the start of the puzzle. To be concrete, let us say that there were no 1s or 2s in the starting grid. Then, in any completion of the starting grid it would be possible simply to change all the 1s to 2s, and all the 2s to 1s, to produce a second valid solution to the puzzle. After making this observation, however, it is already unclear how to continue. Even a simple argument proving the insufficiency of eight clues has proven elusive.
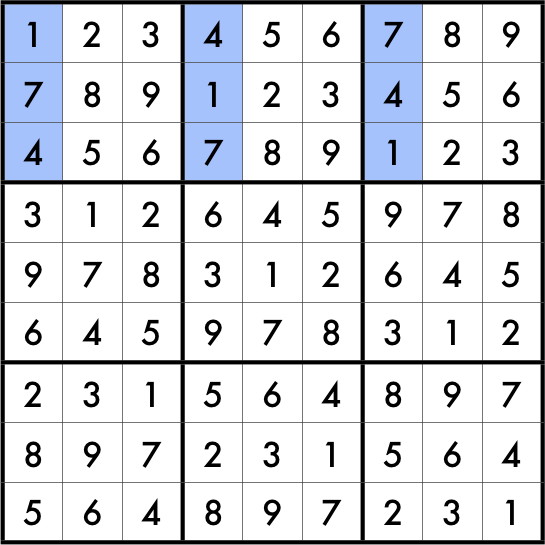
McGuire’s solution requires a combination of mathematics and computer science. To reduce the time required for an exhaustive search he employed the idea of an “unavoidable set.” Consider the shaded cells in this Sudoku square:
Now imagine a starting puzzle having this square for a solution. Can you see why we would need to have at least one starting clue in one of those shaded cells? The reason is that if we did not, then we would be able to toggle the digits in those cells to produce a second solution to the same puzzle. In fact, this particular Sudoku square has a lot of similar unavoidable sets; in general some squares will have more than others, and of different types. Part of McGuire’s solution involved finding a large collection of certain types of unavoidable sets in every Sudoku square under consideration.
Finding these unavoidable sets permits a dramatic reduction in the size of the space that must be searched. Rather than searching through every sixteen-clue subset of a given Sudoku square, desperately looking for one that is actually a proper puzzle, we need only consider sets of sixteen starting clues containing at l
Blog: Topsy Turvy Land - Donna J. Shepherd (Login to Add to MyJacketFlap)
JacketFlap tags: children, Kids, Father, Donna Shepherd, coloring page, Hidden Pictures, Liz Ball, Puzzle, Teacher, Father's Day, Add a tag
Liz Ball shares a hidden picture puzzle and coloring page for Father's Day. To order books with her hidden picture puzzles or other books (like Topsy Turvy Land) from Hidden Pictures Publishing, click HERE. Enjoy! *Click on the picture, then print! It will print out full size ready to be colored. If that doesn't work with your printer, right click on the picture, and then 'save picture as...'
Blog: OUPblog (Login to Add to MyJacketFlap)
JacketFlap tags: slideshow, The Oxford Comment, oxford comment, Will Shortz, *Featured, Lexicography & Language, Audio & Podcasts, Caleb Madison, crosswords, JASA, caleb, sundays, impressively, podcast, Reference, wordplay, crossword, Dictionaries, puzzle, oxford english dictionary, Leisure, Add a tag
Want more of The Oxford Comment? Subscribe and review this podcast on iTunes.
You can also look back at past episodes on the archive page.
Featured in this Episode:
Michelle goes on-site with former Oxford intern Caleb Madison, the youngest person to publish a crossword puzzle in the New York Times (at the age of 15). A puzzle by his class at Sundays at JASA: A Program of Sunday Activities for Older Adults was recently published in the New York Times and featured on the Wordplay blog.
Lauren gets a private tour of the OED museum in Oxford with Archivist Martin Maw.
This slideshow features the crossword class in action, and some impressively old printing relics.
(Click the image if you would like to see it larger.)
Blog: Whateverings (Login to Add to MyJacketFlap)
JacketFlap tags: Cartoons & Comics, taj mahal, Chirp!, Owlkids, Links, people, cartoon, comic, Samples, puzzle, paula becker, Add a tag
Here’s something I did for the May 2011 issue of Chirp magazine. It’s obviously the Taj Mahal. It’s interesting how much you learn about something when you have to draw it. A larger version can be seen if you click on the image.
And I’ve included some close-ups, below. Fun, fun, fun, fun, fun, fun, fun…fun.
Blog: Topsy Turvy Land - Donna J. Shepherd (Login to Add to MyJacketFlap)
JacketFlap tags: Donna Shepherd, coloring page, Hidden Pictures, Liz Ball, Puzzle, Teacher, print, Mother's Day, printable, Add a tag
A special treat! A hidden picture puzzle and coloring page for Mother's Day by Liz Ball. To order books with her hidden picture puzzles or other books (like Topsy Turvy Land) from Hidden Pictures Publishing, click HERE. Enjoy! *Click on the picture, then print! It will print out full size ready to be colored. If that doesn't work with your printer, right click on the picture, and then 'save
Blog: Topsy Turvy Land - Donna J. Shepherd (Login to Add to MyJacketFlap)
JacketFlap tags: children, Kids, Picture Book, book, Donna Shepherd, Puzzle, Teacher, donna j. shepherd, Word Search, Kit Grady, Bradybug, Add a tag
Click on puzzle to enlarge and print. Illustrator Kit Grady's blog: Click HERE.
Blog: Topsy Turvy Land - Donna J. Shepherd (Login to Add to MyJacketFlap)
JacketFlap tags: children, book, crossword, homeschool, Kevin Scott Collier, Donna Shepherd, Puzzle, Teacher, no more gunk, donna j. shepherd, ouch sunburn, printable, crossword puzzle, guardian angel kids, Add a tag
Click on crossword puzzle to enlarge and print. Click HERE for answers.
Blog: Topsy Turvy Land - Donna J. Shepherd (Login to Add to MyJacketFlap)
JacketFlap tags: Donna Shepherd, coloring page, Hidden Pictures, Liz Ball, Puzzle, St. Patrick, Add a tag
A special treat! A hidden picture puzzle for St. Patrick's Day by Liz Ball. To order books with her hidden picture puzzles or other books (like Topsy Turvy Land!) from Hidden Pictures Publishing, click HERE. Enjoy! *Click on the picture, then print! It will print out full size ready to be colored. If that doesn't work with your printer, right click on the picture, and then 'save picture as...'
View Next 21 Posts



















will it be on iPhone?
Yes, this game will absolutely be available on iPhone in July 2013.