By: Franca Driessen,
on 10/13/2015
Few elementary mathematical ideas arouse the kind of curiosity and astonishment among the uninitiated as does the idea of the “imaginary numbers”, an idea embodied in the somewhat mysterious number i. This symbol is used to denote the idea of , namely, a number that when multiplied by itself yields -1. How come?
The post The real charm of imaginary numbers appeared first on OUPblog.
By: Franca Driessen,
on 10/5/2015
Try googling 'mathematical gem'. I just got 465,000 results. Quite a lot. Indeed, the metaphor of mathematical ideas as precious little gems is an old one, and it is well known to anyone with a zest for mathematics. A diamond is a little, fully transparent structure all of whose parts can be observed with awe from any angle.
The post Diamonds are forever, and so are mathematical truths? appeared first on OUPblog.
By: Sara Pinotti,
on 8/18/2015
What is the purpose of mathematics? Or, as many a pupil would ask the teacher on a daily basis: “When are we going to need this?” There is a considerably ruder version of a question posed by Billy Connolly on the internet, but let’s not go there.
The post Will we ever need maths after school? appeared first on OUPblog.
By: MsLuhks,
on 6/28/2011
Happy Tau Day, the most exciting math holiday you’ve yet to discover! Today, June 28th is 6/28, which contains in order the first three digits of tau (τ), the rival of math’s most popular irrational number, pi (π).
In 2001, Bob Palais wrote an article for The Mathematical Investigator called ,“π is wrong!” In it, he insists that the choice of using π in our mathematical formulas for hundreds of years is no good. He argues that the use of τ would simplify many formulas and its derivation is much more intuitive. (Notice that the symbol resembles that for pi, but with one "leg" instead of two.)
The significance of our beloved irrational number π is that it is equal to the ratio of the circumference of any circle to its diameter--in notation, π = C/d. However, the most defining characteristic of a circle is not its diameter but its radius. A circle is defined as the collection of points on a plane that are exactly the same distance, its radius, from a point, its center. Palais argues that intuition should direct us to the use of a more elegant Circle Constant, tau, where τ is the ratio of the circumference of a circle to its radius--in notation, τ = C/r.
Self-described “notorious mathematical propagandist” Michael Hartl takes the argument even further in his now-famous “The Tau Manifesto,” which he published on Tau Day of 2010, exactly one year ago. He demonstrates with many adapted formulas that the factor of 2 is unnecessary if we incorporate it into the ratio itself. For instance, the periods of basic trigonometric functions f(x) = sin(x), and f(x) = cos(x), are in both cases 2π. Why not change them to tau instead? Palais and Hartl each list numerous other examples from calculus and physics, in which the factor of 2 is rendered obsolete by replacing 2π with τ.
The really intuitive part is revealed if you think of angle measure. How things are done now with π, a half turn of the circle is π radians, and a full turn is 2π radians. Should we adopt τ instead, τ radians would be a full turn, τ/2 radians a half turn, τ/4 radians a quarter turn, and so on.
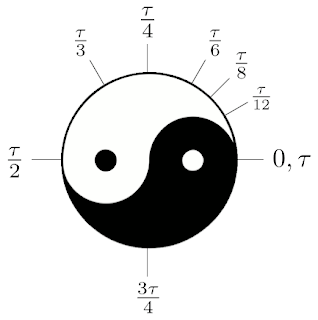
There are, of course, instances where π appears un-doubled. For instance, the formula for area of a circle: A = πr2. Hartl shows, in a mathematically sophisticated way, that the replacement of π by τ even in this instance is the more sound choice, since it is analogous to similar formulas in physics.
An article in today’s BBC News paints the issue as a violent conflict, with pi detractors up in arms over a lifetime of educational betrayal, which seems to this mathematician something of a manufactured controversy. (I can imagine you'd be upset if you are the sort of mathematician that has memorized pi to the nth digit. If you are one of these folks, here's the start for your new parlor trick: reciting tau, 6.283185307...) 
Is it worthwhile to switch to tau use, an
By: MsLuhks,
on 5/11/2011
Last week we offered the Android users among you a selection of free math-related apps. If you’re an iPhone user like I am, you will be pleased to know that there are equivalent apps for your device!
Many of the specific apps for Android are not available on iPhone, but that’s not to say that there is any shortage of math-related iPhone apps. For instance, Andie Graph is not available for iPhone, nor is Graph Lite. However:
• Or if you don’t mind spending $1.99, check out the very nice-looking Graphing Calculator from Appcylon LLC: 
• Algebra 1 Lite is a different mini-interactive textbook: students read some examples and then try out some practice problems. The app also keeps track of student progress. Here’s an example of a quiz question:
By: MsLuhks,
on 3/3/2011
 |
| The Cartesian Plane |
Teachers should expect to be questioned about this: “Why not clockwise?” The stock answer is, “That’s the rule.” Take the time to delve a little deeper. This response may sound to a young person like, “because I say so.” Dissatisfaction with explanations and confusion about them go hand in hand. A solid understanding of how to label the quadrants should enable your students to discuss graphing more efficiently. Graphing on the coordinate plane is a skill that will be immensely valuable throughout high school math and well into college courses, including and beyond multi-variable calculus and electro physics. The purpose of this convention and most conventions in general, is to avoid ambiguity. (And ambiguity can lead to chaos! Imagine if we didn’t have the convention of driving on only one side of the road.) 
Physicists in particular use the right-hand rule to navigate in three dimension
By: MsLuhks,
on 2/7/2011
By: MsLuhks,
on 12/6/2010
I love this story because I think it eloquently demonstrates the following dispositi
Great post. I almost forgot about tau since 6/28 is a special day for me. I guess the debate will go on, but probably not much change.
You have explained this so well! I would like to try replacing pi with tau when I cover circles with my students. It will be a great opportunity for them to take a position and argue it one way or the other.